Synthetic Control

1 Constructing a synthetic control

The following explanation is adapted from Abadie et al. (2010).

$Y_{it}$ is the outcome where $i=1,\dots,J+1$ and $t=1,\dots,T$. $Y_{it}^N$ and $Y_{it}^I$ are the counterfactual outcomes for the untreated and treated. The treated group is denoted by $i=1$ and the control groups (the donor pool) by $i=2,\dots J+1$. The treatment is applied at $T_{0}$ where $1\leq T_{0}<T$.

$W$ is a $(J\times 1)$ vector $(w_{2},w_{3},\dots,w_{J+1})’$ with nonnegative elements. The synthetic control at time $t$ is $\sum_{j=2}^{J+1} w_{j}Y_{jt}^N$. The treatment effect at $t$ is $Y_{1t}^I - \sum_{j=2}^{J+1} w_{j}Y_{jt}^N$.

The key task is to estimate $W$. Consider a $(k\times 1)$ vector $X_{1}=(Z_{1}, Y_{1}^{(1)}, Y_{1}^{(2)},\dots,Y_{1}^{(m)})$. $Z_{1}$ is a vector of covariates for the treated—typically predictors of $Y_{1}$. $Y_{1}^{(m)}$ is a combination of pre‑treatment $Y_{1}$. The most obvious choice is $Y_{1}^{(1)}=Y_{11}, \dots, Y_{1}^{(m)}=Y_{1T_{0}}$, i.e., the $Y_{1t}$ in every pre‑treatment year. Conceptually, $X_{1}$ captures the characteristics of the treated. Note there is no $t$ subscript in $X_{1}$, indicating it is an average over pre‑treatment periods (e.g., average per‑capita GDP).

Now consider a $(k\times J)$ matrix $X_{0}$. $X_{0}$ is similar to $X_{1}$ but captures the characteristics of all units in the donor pool. We estimate $W$ by minimizing:

i.e., minimizing the distance in characteristics between the treated and the synthetic control. $V$ is typically a semi‑positive diagonal matrix whose elements determine the importance of each covariate in $X$. $V$ is chosen by:

where $Z$ is the pre‑treatment trajectory of $Y$, i.e., $Z_{1}=(Y_{11},\dots,Y_{1T_{0}})$. Eq. (2) says $V$ is determined by minimizing the prediction error of the outcome.

Once $V$ is given, compute $W$ with Eq. (1).

2 Placebo falsification

2.1 Placebo states

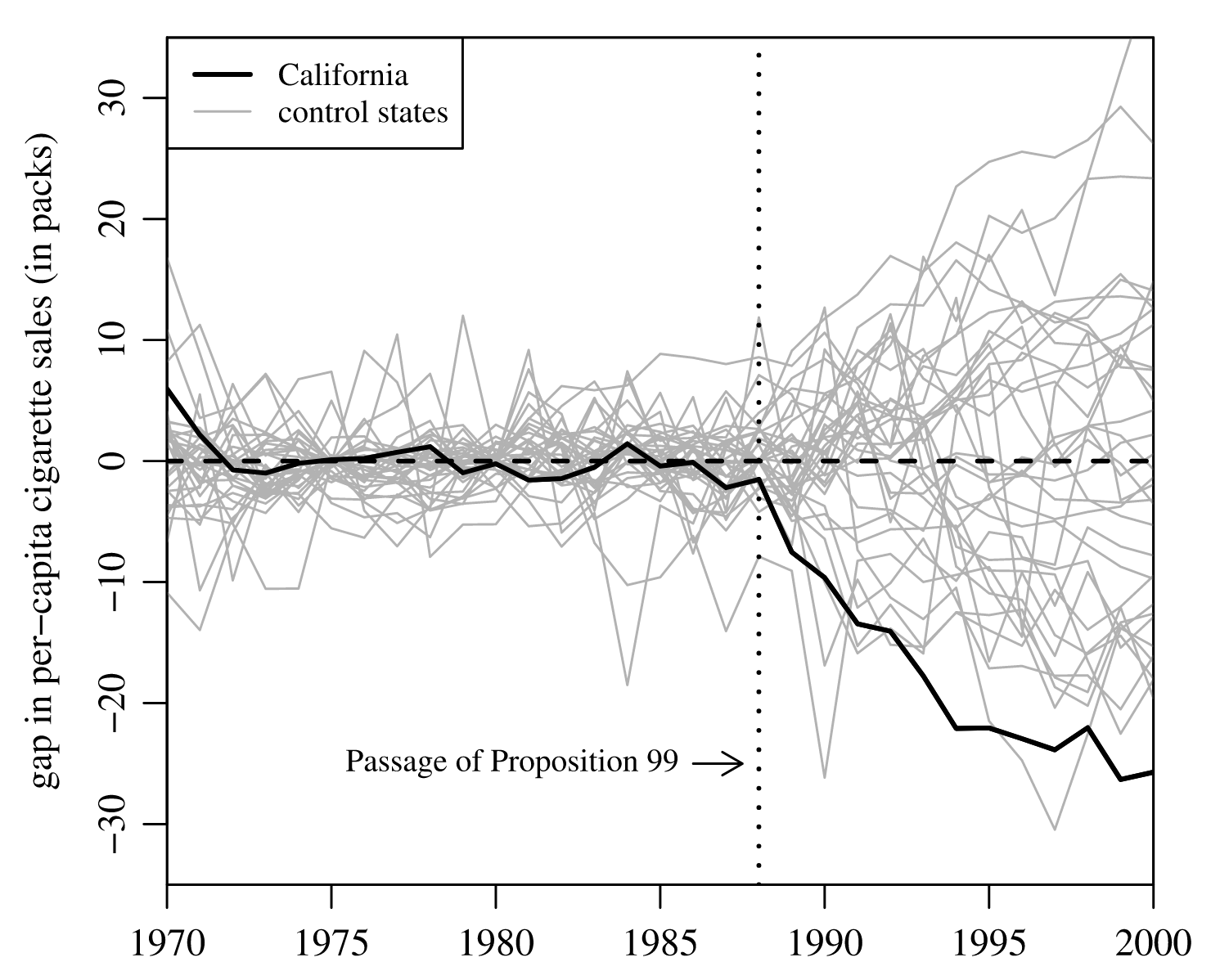
Fix the treatment date and randomly shuffle the treatment states. In the California Proposition 99 case (Abadie et al., 2010), the treatment date is 1988, the treated state is California, and there is a donor pool. For a placebo test, the authors:

“In each iteration we reassign in our data the tobacco control intervention to one of the 38 control states, shifting California to the donor pool. That is, we proceed as if one of the states in the donor pool would have passed a large-scale tobacco control program in 1988, instead of California.”

Then re‑estimate the model and plot the real and synthetic cigarette consumption before and after the treatment date:

As seen in the figure, California lies on the extremely negative side of the distribution.

For a numerical test, compute:

1. Pre‑treatment prediction error (e.g., $\sum_{t=0}^{T_{0}} (Y_{1t}-\sum_{j=2}^{J+1} w_{j}Y_{jt})^2$, measured as MSE)
2. Post‑treatment prediction error
3. The ratio of post‑ to pre‑treatment MSE
4. Use the distribution of ratios to compute the p‑value for the treated state

2.2 Placebo dates

Keep treated and untreated states fixed, but choose different treatment dates (typically pretreatment dates). Example: Abadie, Diamond, and Hainmueller (2015).