The Implicit Prior of Deep Learning

1 Background

I’ve been recently exploring the connections between deep learning and Bayesian statistics, particularly how neural network architectures and optimization algorithms encode implicit priors over the parameter space. Through these explorations, I discovered a fascinating insight: SGD (stochastic gradient descent) doesn’t actually search uniformly over all possible parameters. Instead, the architecture, initialization, and optimization algorithm together impose strong Bayesian-like priors that fundamentally shape the learning process.

This got me thinking: most people (including myself initially) imagine neural network training as exploring a vast parameter space uniformly, trying different parameter configurations until finding a good solution. But that’s a misconception. The network architecture, initialization scheme, and SGD algorithm together impose strong implicit priors that dramatically constrain where the search actually happens.

2 Visualizing the Insight

I wanted to create a simple visual to illustrate this gap between intuition and reality. I generated two diagrams showing the same parameter space with a red dot representing the optimal parameters (or a good solution).

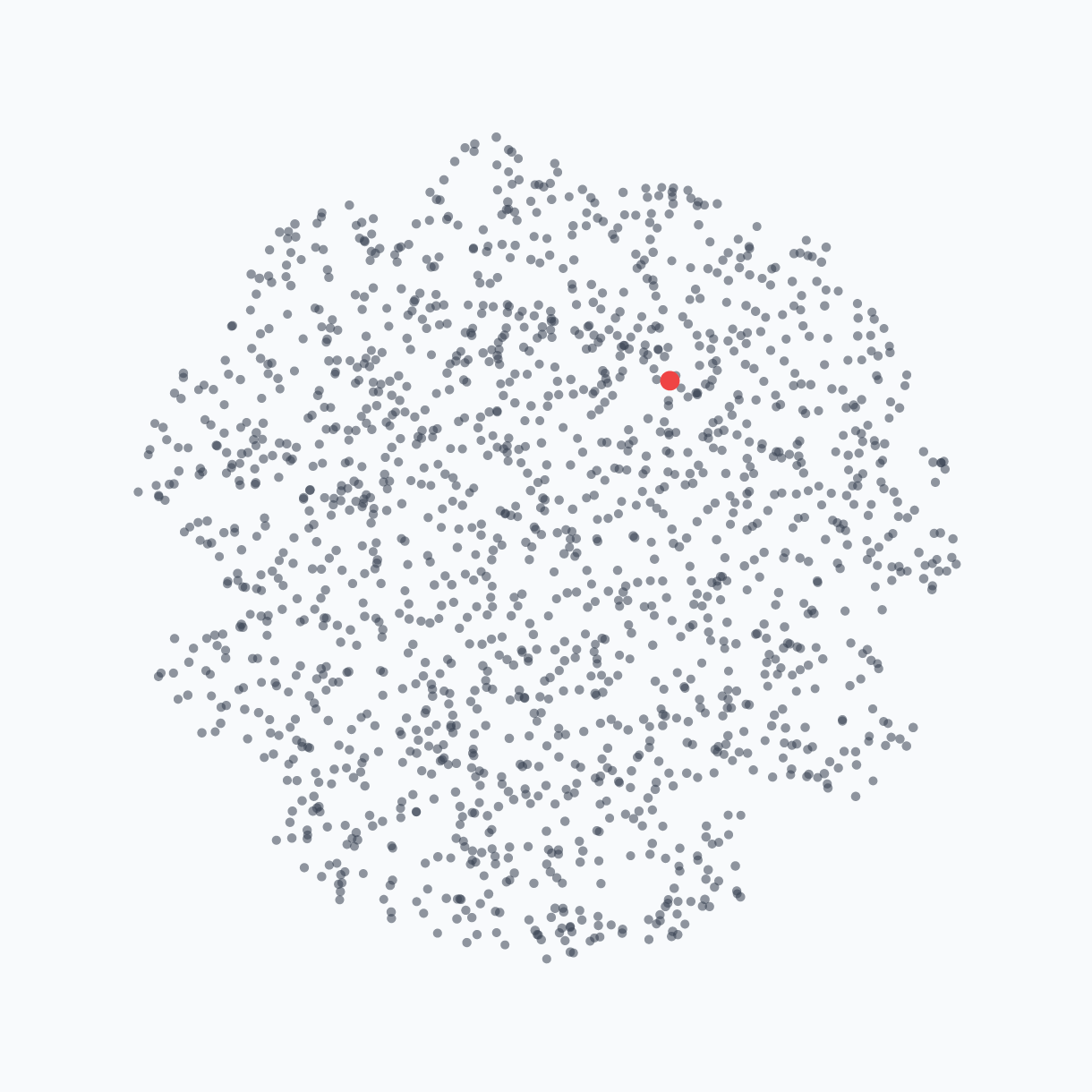
The naive intuition: How do you think a deep neural network searches for optimal parameters? Each dot represents a possible parameter realization. The density of dots represents the prior — how likely we believe the parameters will be at different locations.

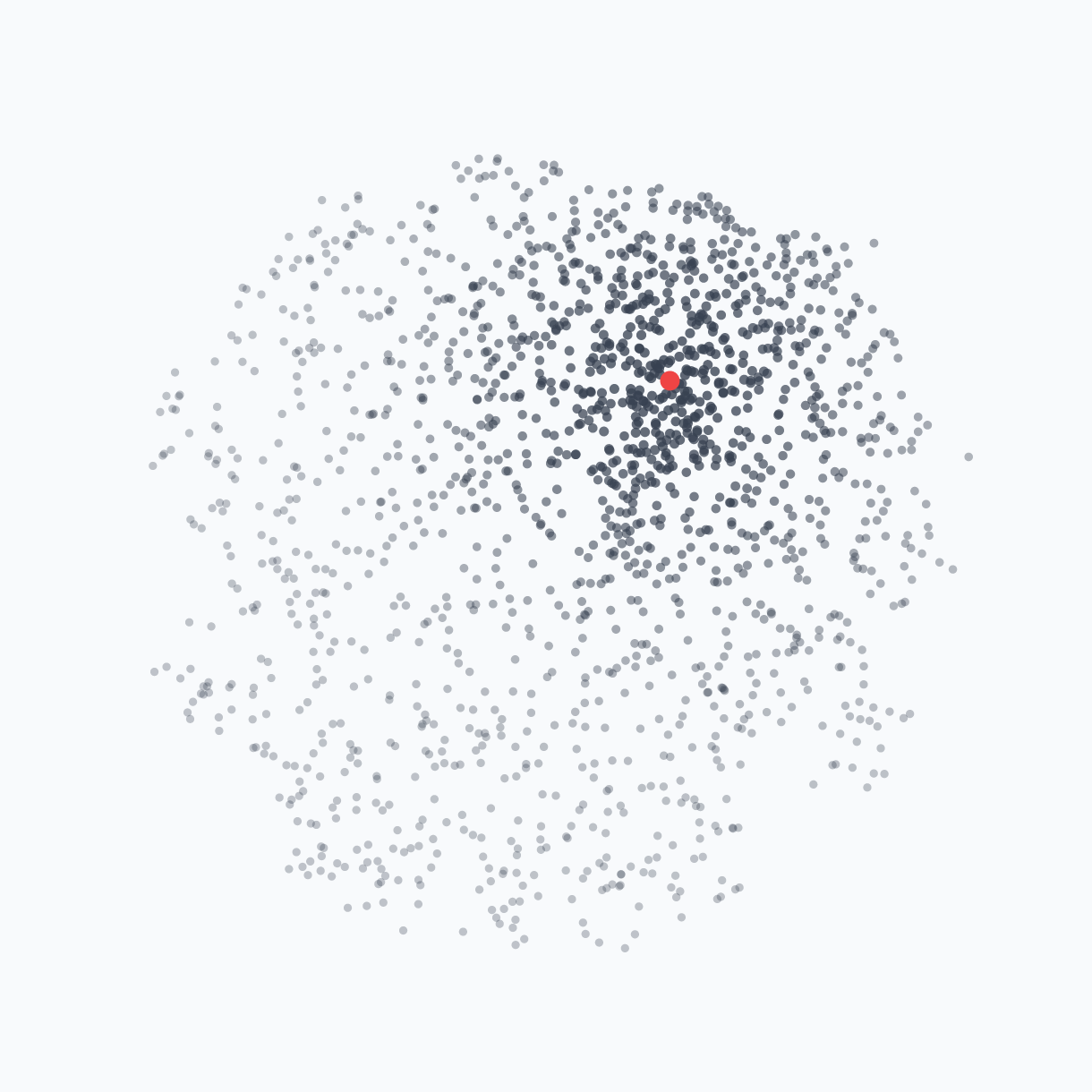
The reality: But this isn’t how deep networks actually search for optimal parameters. The prior is not uniformly distributed. Surprisingly, the network architecture and SGD strongly prefer certain parameter realizations over others, creating an implicit bias that concentrates the search around specific regions.

3 Why This Matters

This implicit bias is actually a feature, not a bug. It’s part of why deep learning works so well — the inductive biases encoded in the architecture and optimization help guide the search toward solutions that generalize. Understanding these implicit priors is crucial for:

• Designing better architectures
• Choosing appropriate initialization schemes
• Understanding why certain hyperparameters work better than others
• Explaining phenomena like the lottery ticket hypothesis

The parameter space isn’t just high-dimensional — it’s structured, and our tools exploit that structure in subtle but powerful ways.